Designing an Aircraft Propeller For the Martian Atmosphere
Overview
The purpose of this example is to demonstrate the usage of arbitrary fluids/gases by considering a propeller design for an aircraft designed to fly through the martian atmosphere. You should probably open the martian_aircraft_propeller.prp project (in latest release) and follow along to get the most out of this walkthrough.
Based upon the success of NASA's Helios Prototype, it seems like aerodynamic flight on Mars is well within the realm of physics and human ingenuity... practicality, cost, how to get the thing aloft are entirely different issues. The Helios prototype flew on solar/battary power at an altitude of ~100,000 feet. At this altitude the air density is 0.0167 Kg/m^3, which compares closely to Mars at 0 feet (0.013 kg/m^3).
First Things First
When PropGen starts up, it defaults to an ISO Standard Atmosphere, so that's the first thing we need to change. In *both* the CREATE DESIGN and COMPUTE PERFORMANCE panels click "Not using Std Atmosphere" in the "Basic Data" tab. You should be good to go with arbitrary fluids now (see selecting_alt_fluids if this is not clear).
Gather The Fluid Properties
For non-terrestrial atmospheres, PropGen requires density (ρ), kinematic viscosity (ν), and sound speed. Kinematic viscosity is derived from dynamic viscosity (μ)via the formula: ν = μ / ρ.
The Martian atmosphere is ~95% CO2, but for our purposes we'll assume 100% CO2. This makes it easy to get dynamic viscosity using, for example, the gas viscosity calculator from LMNO engineering. We'll pick a "nominal summer flight temperature" of +5 degrees Celcius, which gives a dynamic viscosity of μ = 1.422e-5 kg/m-s.
To get density we'll assume a flight altitude ~0 ft, and use NASA's well known Mars Atmospheric Model:
a) ρ = p / (0.1921 * (T + 273.1)), T = degrees C
b) p = 0.699 * e-0.00222h, h = altitude in meters
==> plug in the numbers and get:
ρ = 0.01308 kg/m3, and
ν = 0.0010868 m2/s (= 1.422e-5 / 0.01308)
The 3rd and final fluid property we need is sound speed. For CO2 at 5 °C this works out to ~262 m/s.
Gather Your Design Constraints
You'll also need to specify your geometric properties, and operating conditions. I did some "back of the envelope" calculations to come up with initial some numbers. These are within the martian_aircraft_propeller.prp sample project included with the latest distribution.
Create An Initial Design
Open the martian_aircraft_propeller.prp sample project and click the CREATE DESIGN button. After a short while an inverse design html file should pop up. The design should look like figure 1. This has a few kinks in it, and areas of subtle curvature can probably be linearized to keep things simple.
Figure 1:
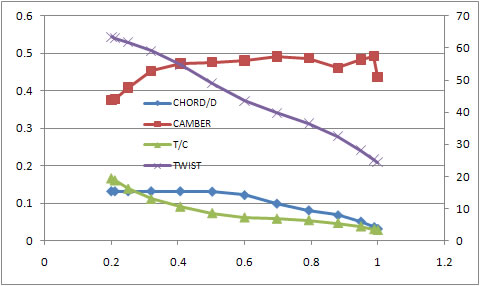
You'll also notice the Reynolds numbers are ~30k. NACA65 are most certainly not suitable for such a design... you should use low Reynolds number laminar airfoil sections. If you have a dataset for such airfoils feel free to submit them using this format.
Manually Refine the Design
Manually refine the geometry as described above and enter it into the "Geometry Definition" tab (this has already been done for you in the sample project).
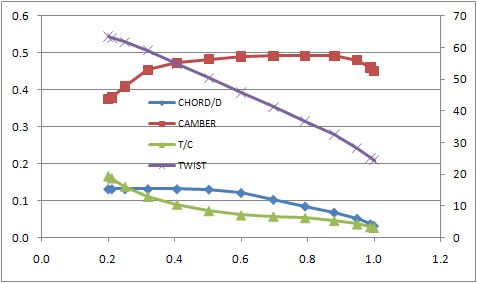
Enter various power (or thrust or blade angle) settings to get a feel for the overall characteristics of your design. Click COMPUTE and PropGen will pop up an html file when it's done crunching numbers.
Will A Martian Aircraft Every Fly?
I believe given enough money an unmanned aircraft is well within the realm of human ingenuity. NASA's already demonstrated solar powered flight at 100,000 ft, where the air is about as thin as that on Mars. Of course Mars is 1.5x further from the sun and so the solar energy will be ~0.33 that of earth, but much of that deficit can be overcome with more efficient solar panels (Helios panels were only 20% efficient). Also, Mar's gravity is 1/2.64 that of earth which should give a small reduction in induced drag compared to what you'll get on earth at 100,000 ft.
References
http://www.nasa.gov/worldbook/mars_worldbook.html
http://en.wikipedia.org/wiki/Climate_of_Mars
http://www.lmnoeng.com/Flow/GasViscosity.htm
http://www.grc.nasa.gov/WWW/K-12/airplane/atmosmre.html
http://www.nasa.gov/centers/dryden/news/FactSheets/FS-068-DFRC.html